[TKDE23]Enabling Privacy-Preserving and Efficient Authenticated Graph Queries on Blockchain-Assisted Clouds

本文解决的是区块链上查询的隐私保护和高效验证的问题，这两个问题在区块链上已经得到较为广泛的研究，并且支持的查询类型也有键值查询和范围查询，但是本文是第一个在图数据上解决这两个问题的工作。同时本文提出文章的**主要挑战是如何设计一个支持认证查询的认证数据结构(ADS)**，本文的解决方案同vChain类似都是构造一个累加器来解决认证问题，不同点在于隐私保护问题的解决。文章的贡献可以归纳如下：

• 设计了一个兼顾隐私保护和高效验证的ADS，PAGB。同时引入批量验证和二叉树求积的方式进行验证过程的优化。
• 首篇在属性图上做ADS的工作，将图的属性建模进累加器中，为区块链上图数据存储及其认证查询提供了一个新的范式。

摘要

之前的研究引入了区块链辅助云的新场景，数据所有者将原始数据外包给云服务器，并在区块链上存储一些元数据。尽管在这种混合存储场景下对键值查询和范围查询进行了一些研究，但其他更复杂的数据类型还不被支持。在本文中，我们在区块链辅助云上对图形数据的认证查询进行了开创性的研究，由于许多新兴的应用，图形数据是一种流行的数据类型。**主要的挑战是如何设计一个支持认证查询的认证数据结构（ADS）**，并能被区块链轻松维护。为此，我们提出了一种新型的ADS，名为PAGB，基于RSA累加器和完备性集。它还可以防止原始数据通过区块链或不相关的查询泄露给公众。我们进一步优化我们的设计，使其在通信和计算方面更加高效。PAGB的有效性和效率通过理论分析和大量实验得到了验证。

引言

由于区块链技术的出现，智能合约为可信存储和可信计算环境提供了一个新的范式。一些数据所有者选择在区块链上存储数据作为云服务器的补充。然而，由于有限的存储空间和过高的气体成本，直接在链上存储原始数据几乎是不可行的。解决这个问题的一种方法是采用区块链辅助云，如图1所示，采用链上存储和链下存储。数据所有者仍然将其原始数据外包给云服务器等链外存储，但只在链上存储一些元数据（如原始数据的哈希值）。为了确保从不受信任的链外存储中获取的数据的完整性，可以利用链上元数据来验证查询结果。

在云上引入区块链最重要的是解决外缘数据的新鲜度问题，若不解决会收到重放攻击(Reply Attack)，元数据上区块链云可以保证ADS的完整性和新鲜度。

一些主要的查询类型，如键值查询、范围查询和文件关键字查询，已经得到了很好的研究。然而，作为另一种重要但更复杂的数据结构，**图数据还没有被支持**。由于许多基于图模型的新兴应用，如社交网络、生物网络、医疗保健和知识管理，图数据已经引起了巨大的兴趣。采用上述的混合存储模式，数据所有者可以借助云服务器来存储和管理图数据。同时，元数据将从他们的原始数据中产生，并被发送到区块链上。这样一来，从云端获得的查询结果的完整性就可以根据区块链维护的可信ADS进行验证。

为了在区块链辅助的云中提供对图数据的认证查询，有几个挑战摆在面前：（1）ADS需要是轻量级的，并且可以由区块链轻松维护，因为区块链的存储和计算成本很高。传统的方法，如基于树的ADS和聚合签名，由于不支持动态数据，所以需要大量的存储和更新时的过度修改。因此，这些方法不再适用于区块链。(2）查询结果通常要满足正确性和完整性的要求，后者要求没有有效的答案遗漏，这使得认证设计更加困难。传统的基于Merkle Hash Tree（MHT）的ADS[5]，[8]没有能力为一个元素提供不存在的证明，例如，证明被查询的节点没有向外的边。(3)隐私保护， 除了对查询本身的了解，云和区块链不能向用户透露任何无关的信息，因为可能有一些对隐私敏感的数据不能公开。

为了应对这些挑战，我们设计了一种新型的ADS，名为Privacy-preserving Accumulator for Graphs in Blockchain（PAGB），它在区块链辅助云中提供对图数据的认证查询，同时保证查询结果的合理性和完整性。我们以属性图[9]为例来说明其有效性，属性图是由知识图表示的一种图类型，在人工智能领域具有巨大的潜力。为了满足结果的完整性和隐私保护的要求，我们构建了一个完整性集，从原始图中提取**不相干的对**，这样就可以证明一个项目的不存在。在区块链方面，我们计算每个对象的**质数代表**作为元数据来更新其累积器，这也阻碍了潜在的隐私泄露。为了进一步提高效率，我们通过降低验证成本和加速乘法过程来优化解决方案。

贡献：

• 我们首先在区块链辅助云的场景下，对属性图数据的认证查询问题进行了阐述。
• 我们在完备性集合和动态累加器的基础上设计了一个隐私保护的ADS，称为PAGB。然后我们提出了满足一些查询的合理性和完整性的认证查询处理算法。
• 我们进一步通过纳入非交互式协议和设计二进制树形乘法使设计更加实用。
• 我们正式分析了该设计，并进行了广泛的实验来评估其性能，这表明了我们设计的有效性和效率。

预备知识

加密累加器，加密累加器是一个单向的、抗碰撞的结构，它将一个集合映射到一个固定大小的摘要中。根据底层合约的实现，加密累加器通常可分为RSA累加器和双线性映射累加器。RSA累加器采用RSA模数(modulus)的模块化指数计算，而双线性映射累加器则采用椭圆曲线运算。我们在本文中选择的RSA累加器的一个特点是，它可以通过生成相应的Proof来证明一个任意元素的存在性证明。 \(Ac=g^{x_p} \ mod \ n\) 其中𝑋为素数集，𝑥𝑝为𝑋中所有元素的乘积。

• MembershipWitness(𝑥)

• VerifyMembership(𝑥, 𝜋)

• NonmembershipWitness(𝑥)

• VerifyNonmembership(𝑥, 𝑎, 𝑑)

还有非交互式指数证明和非交互式指数知识证明

问题陈述

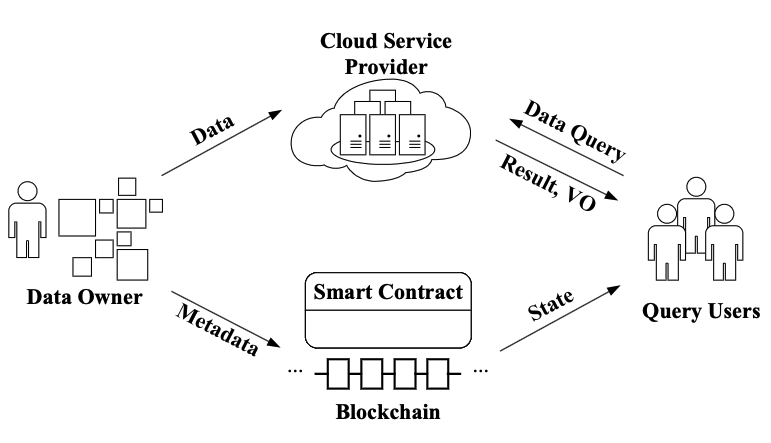
如图所示，系统中存在四类角色，分别是DataOwner（DO）、CloudServiceProvider（CSP）、BlockChain（BC）和Users。其中CSP和BC都存有可验证数据结构（ADS），CSP中的ADS用于生成验证对象(VO)，BC中的ADS利用智能合约的真实性来提供可信状态。

**属性图**，在本文中，我们将聚焦属性图来阐述解决方案，同时我们的设计同样适用于普遍的有向图。我们将属性图建模为$G=(V,E)$，每个在V中的节点都有一个或多个属性（例如，名称，链接等），这些属性通常能够用键值对集合来表示，因此一个节点v能被表示为$(id, [<na_k,nav_k>])$，其中id表示的是节点的标识符，$na_k$表示的是属性名，$nav_k$表示对应的属性值。用$e=(v_i,v_j)$表示一条由节点$v_i$指向$v_j$的边，每条边也有对应的边属性$(v_i,v_j,type,[<ea_k,eav_k>])$，其中type表示边的属性。本文涉及的可验证属性图查询类型主要有：

• 节点属性查询
• 边属性查询
• 连接度查询
  • $outbound(v_i,[type_k],K)$：返回所有$v_i$能够在K步之内到达且边的属性符合$[type_k]$的终点节点。
  • $inbound(v_i,[type_k],K)$：返回所有能够在K步之内到达$v_i$且边的属性符合$[type_k]$的气势节点

作恶场景

DO和BC被视作可信参与者；User可能因为想要知道查询结果以外的数据而作恶；CSP虽然不太关心数据，但是可能会对查询结果作恶，原因可能是为了节省资源、磁盘错误、软件错误等。由此CSP需要返回VO来验证查询结果，User通过与BC中的ADS进行比较可以验证查询结果的正确性和完整性。

要完成图式数据的查询过程和验证过程需要在设计ADS的时候满足以下几点：

• 动态性。应支持数据的动态性，包括对外包数据的插入、删除和更新操作。
• 隐私保护。我们假设我们的模型中的CSP在隐私方面是可信的。BC是可信的，但可能会被动地泄露信息，因为它是可公开访问的。因此，原始数据只能从DO和CSP中获取，否则会发生隐私泄露。此外，除了查询本身所需的知识外，查询用户不能得到图的任何无关信息。
• 效率。效率体现在以下三个方面。1）气体(gas)效率。智能合约需要花费合理的气体来维持BC中的ADS。2）通信效率。保证数据完整性的验证方案会产生很小的网络带宽使用量，即𝑉𝑂的大小很小。3）计算效率。ADS维护、VO生成和VO验证的时间成本可以接受。

为图数据设计的PAGB

PAGB构建

我们的PAGB构造主要由四个阶段组成，即初始化、完整性构造、素数表示和累积。构建过程包括DO、CSP和BC的参与。在构建过程中，DO在本地执行所有四个阶段，然后将构建的ADS交给BC。CSP也进行积累以维护ADS。

初始化

设置阶段的目标是生成PAGB中使用的公钥和秘钥。它最初由DO进行，只进行一次。DO调用密钥生成算法$KeyGen(1^{\lambda})$，其中𝜆是安全参数，以获得系统参数，即p、q、n和g。这里n=pq，其中p和q都是素数，具有相同的长度。在四个参数中，p和q属于秘钥，只由DO生成和保存。剩下的n和g是公钥，所有各方都可以使用。

完整性构造

完整性构建阶段旨在生成完整性元素，以便在保证结果完整性的情况下，每个查询的信息泄露可以限制在答案本身。例如，假设我们已经将节点$(id, [<na_k,nav_k>])$存入PAGB。然后，用户希望通过发出节点属性查询，即节点属性$(id,na)$，来获得节点v中$na$的属性值。但实际上节点v并没有$na$这个属性。直观地说，CSP需要返回v及其成员见证作为VO来说服查询用户相信$na$不存在。因此，v的所有信息都透露给了查询用户，而𝑣的所有属性与查询无关。用户可以得到关于图数据的外在知识，这就违反了隐私保护的原则。为此，CSP需要给出$(id,na)$及其非成员作为VO，这样才能同时保证结果的完整性和隐私保护的特点。为了进一步覆盖所有的查询类型，我们提出了完整度构建算法。

该算法创建了一个完整性集合$C$，以容纳认证查询类型所需的所有完整性元素。它提取每个节点的标识符$id$、每个属性$(id,na)$和每个属性-值对$(id,na,nav)$。同样，对于每条边，标识符$(v_i,v_j,type)$、每个属性$(v_i,v_j,type,ea)$和每个属性-值对$(v_i,v_j,type,ea,eav)$也被添加到这个集合。此外，我们还记录了$(v_i,v_j)$，节点出度类型$(v_i,out,type)$，节点入度类型$(v_j,in,type)$，每一对的所有类型$(v_j,v_j,[type_k])$，所有节点出度类型$(v_i,out,type,[v_k])$和所有节点入度类型$(v_j,in,type,[v_k])$。

素数表示

累加器的输入域必须是素数，由于上一阶段生成的节点、边和完整性的集合都是几个对象的任意元组(tuple)，我们需要通过素数表示阶段将这些元组映射为素数。在本文中，我们通过随机预言机算法$H_{prime}(·)$生成随机素数代表，该算法计算一个输入的素数代表。它首先用保留符号依次串联对象，并将其转换为一个字符串，在此基础上可以产生一个哈希值。然后，哈希值可以被转换为相应的整数，输出的素数是不小于该整数的最小素数。

累积

累积阶段旨在生成ADS状态，即累积器的累积值，用于查询认证。该算法首先计算所有元素的乘积，然后计算累积值Ac。在BC侧，它将产生Ac并直接交给BC作进一步维护。至于CSP方面，该算法将首先把节点集和边集存储到图数据库中进行正常搜索。然后他也会计算出自己的ADS状态$Ac^∗$，并将其发送给BC。在收到来自DO和CSP的两个积累值后，BC将通过与来自DO的可信Ac进行比较来检查CSP的$Ac^∗$是否有效。如果有效性通过，BC将在智能合约上存储Ac以及公钥n和g。$\phi(n)=(p-1)*(q-1)$可用于加速累积过程。

可验证查询过程

在本小节中，我们描述了目标图查询的查询处理和结果验证，即节点属性查询、边缘属性查询和连接性查询。需要指出的是，我们在本文中只解决了验证方面的挑战。图数据在数据库中的存储和数据查询的效率超出了我们的工作范围，因为已经有一些成熟的图数据库可用。

在高层次上，认证查询处理的设计原理是给出查询所需的确切水平的答案。如果对象存在，那么将返回成员资格。否则，在不透露其他额外信息的情况下给出不存在的答案。我们还定义了相应算法所揭示的泄漏函数。

优化

在本节中，我们提出了两种优化方法，即批量验证和乘法计算，以减少实践中的时间成本和网络开销。

VO大小过大不仅影响通信成本，而且对于计算而言时间成本过大，因此引入了批量验证来降低VO和计算成本。

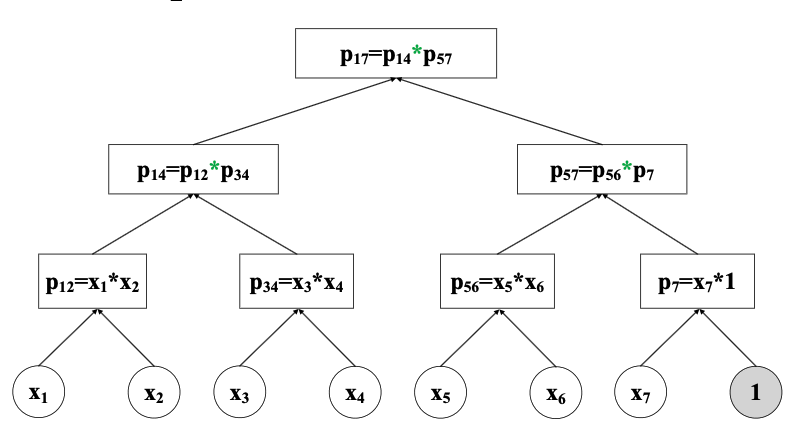
对于乘法计算，有两类常见的计算法则，grade-school算法和Karatsuba算法，但这两类连乘算法在遇到具有大数的数据集时会变得非常慢，这是因为大数通常占用了太多的比特位。本文提出一种二进制数连乘算法如图所示，将数扩充到最小的$2^n$，不够的数字用1代替，如图中有7个数字则填充到8位并用1表示，其中黑色的乘法用grade-school算法，绿色的用Karatsuba算法。

实验

在本节中，为了更好地证明我们设计的有效性和效率，我们对DO、CSP和查询用户进行了评估。此外，我们在Solidity中构建了一个智能合约，并将其部署到以太坊官方测试网络𝑅𝑖𝑛𝑘𝑒𝑏𝑦。我们在一台配备i9-9900K CPU、32GB内存和1TB SSD的机器上运行实验。所有的测试都是用Python 3.8.0编写的，并且只在一个CPU核心中进行，而不是并行地评估最坏的情况。如果应用于实际系统，我们的设计能够通过并行计算迅速加速。在我们的实验中，我们选择了三种真实世界的图数据集，即ca-CondMat2、cage153和ConceptNet54，来全面评估我们设计的性能。在我们的RSA累加器生成中，公钥n被设置为256位，素数代表被限制为128位整数，这不是绝对安全的，但对于正常应用来说已经足够了。

相关工作

据我们所知，目前还没有研究区块链场景下属性图数据的认证查询的研究工作。我们的设计与以下两类研究有关。第一类是现有的关于传统图数据查询认证方案的设计，第二类是我们研究的在区块链之上的认证查询工作。

图上的认证方案

对图数据的认证研究通常集中在ADS的设计上。Martel等人提出使用MHT对树进行认证，并将其扩展到有向无环图。Goodrich等人采用散列方案和数字签名方案来验证图数据。然而，散列方案可能会泄露隐私，因为散列的验证涉及其他未共享的图数据的散列值。为了解决隐私泄露的问题，Arshad等人介绍了一种与树状表示相结合的抗碰撞散列方案。散列方案的一个主要缺点是，对图数据的一些更新通常会产生惊人的计算成本。Goodrich等人还引入了路径散列累加器来解决路径属性查询和路径搜索问题。Zhu等人将加密累加器与数字签名方案相结合，为图提供隐私保护的认证。Kundu和Bertino提出了一种使用树形遍历和聚合签名的结构性签名。基于可编辑的签名，de Meer等人利用累加器构建了一个可证明的安全方案，能够编辑任何节点。Camacho和Hevia利用相同前缀证明给出了一个基于散列法的有向树的高效解决方案。

区块链上的认证查询

区块链中的认证查询，能够对区块链数据或外包给区块链的数据进行完整性验证，近年来正成为一个热门话题。一些研究工作，如BigchainDB，EtherQL利用传统数据库来促进对区块链数据的有效查询。然而，这些设计不能保证数据的完整性，因为查询结果可能与区块链数据不一致。VQL提出将数据库的指纹写入区块链，这样数据库就可以被信任。为了实现对区块链数据库的可验证查询，Xu等人提出了一个新颖的vChain框架，该框架采用了累加器作为其验证数据结构。也有一些作品利用区块链为外包数据提供可验证的查询服务。Hu等人提出了一种基于智能合约的新型可搜索加密方案，以确保查询结果的正确性。然而，该设计仅局限于文件关键词搜索，而且在区块链中存储大量原始数据的成本很高。Zhang等人提出$GEM^2-Tree$在混合存储区块链的情况下提出了一种节省gas费用的ADS。然而，所提出的树状结构只支持键值对的范围查询，并且它们的键可以通过智能合约透露给公众。

结论

在本文中，我们迈出了第一步，研究了区块链辅助云上财产图数据的认证查询问题。为了解决认证查询和隐私泄露的挑战，我们提出了一种新型的ADS，名为PAGB，它可以很容易地由区块链以低成本进行维护。区块链可以完美地保证ADS的新鲜度和完整性。我们凭借非交互式协议和二叉树乘法，进一步提高了效率。我们的设计拥有动态和隐私保护的理想特征，理论分析和原型实现证明了其有效性。

我们的工作为区块链上的图数据存储及其认证查询提供了一个前所未有的范式。它为区块链上复杂数据结构的存储开辟了一个新的方向。我们设计的主要限制是，我们假设CSP不会泄露任何数据，因为外包数据是原始的而不是加密的。此外，我们可以支持的图数据查询类型不包括一些涉及数值的复杂查询，例如最短路径查询。在未来，研究如何支持加密数据和数值的查询认证将是非常有趣的。